
![]()
 |
|
|
|
|
Intusoft Newsletter Issue
#41, April 1995
Copyright ©2002
Intusoft, All Rights Reserved
| In This Issue | |||
| 1 | New Products at DAC | 4 | Mac Users Abandoned |
| 2 | Simulating Digital Filters and Systems | 5 | New MP SPICE |
| 3 | Mixed Environment Simulations | 6 | Current Mode Design with Current Conveyers |
At this year’s Design Automation Conference, Intusoft will introduce and demonstrate several new products including:
The Array Processing Code Model Library, APCML, provides a variety of new array processing functions for use with the ISSPICE4 simulator. Many of these functions have never been available in SPICE before. The APCML also provides a generalized OLE 2.0 interface for users to add their own OLE 2.0 in- process servers.
ISSPICE4 supports digital circuits using an embedded event driven simulator. This capability is fully integrated with the analog transient analysis enabling any mixed mode system to be described by a single schematic design. No cumbersome co-simulation backplane is needed. In addition, the event driven simulator uses a general purpose algorithm that is not limited to digital elements. Both non-digital signals and models created with C code subroutines can be simulated. The Intusoft Code Modeling Kit (CMSDK) allows you to create your own alternate signal types and models. The “User Defined Signal” allows models to pass arbitrary data structures without the need for conversion to a pre-defined signal type (analog, digital, etc.). Digital simulation in ISSPICE4 is actually implemented as a special case of this user-defined signal capability where the digital state is defined by a data structure that holds a logic state and strength value.
The combination of the user-defined signal, C code model, and the event-based simulation capabilities allow ISSPICE4 to support mixed-level, as well as mixed-signal simulation. This new approach to modeling and simulation is the foundation of the sampled-data system models included with ISSPICE4. They also give a small indication of the power of the CMSDK. This article discusses the use of these new models in two digital filtering applications.
The digital approach to filtering offers several advantages over analog implementations. These include stable and repeatable performance, greater programmability, and filtering at ultra-low frequencies not practical for analog methods. The theory behind various digital filter design techniques is covered in several references [1-3]. Here, we will concentrate on the ISSPICE4 implementation.
Continuous time signals can be
represented by Laplace transforms or linear differential equations.
In a similar manner, the z transform can be used to describe a
sampled-data system in the form of linear difference equations.
To realize difference equations using z transforms three basic
elements (Figure 2) are needed: delays,
multipliers, and summers. The multiplier and delay elements operate
using real-valued
data that only changes when an event occurs. This “real”
signal is not “analog” because it only changes at certain
times and it s not “digital” because it has a floating
point value. Use of this methodology minimizes the amount of calculations
that must be made; greatly improving performance. The z-1 element
delays its input by T seconds. T is the sampling period set by
the digital clock signal. The representation used for a sampled
delay arises from the fact that the z transform of x(n-1) is simply
z-1 times the z transform of x(n). The z transform delay can also
be built with an ideal transmission line [4]. This approach is
efficient for designs using less than 5-10 delay elements. For
SPICE 2 based programs, however, the transmission line can use
excessive amounts of memory and run slowly. Fortunately, these
transmission line problems have been fixed in ISSPICE4.
When ISSPICE4 simulates digital
gates, the highest logic level and strength determine the status
of a node when two or more outputs are connected. For real nodes,
a “resolving” function in ISSPICE4 causes the outputs
of all real elements to be summed. Therefore, the summing operation
is performed automatically by simply connecting two or more outputs
together. “Node Bridges” are used to connect nodes of
different types. For example, the input analog signal is sampled
by the analog-to-real bridge. A digital clock running at the sampling
period is used to sample the data and clock the delay elements.
Note that C code models can have one or more ports with different
node types. Hence, a bridge is not needed for the delay’s
clock input because a digital signal is expected. The filter output
is
converted to an analog signal using a real-to-analog bridge. The
multiplier, delay, and bridge elements are C code models created
by Intusoft with the CMSDK. A new analog-to-real model was developed
to support this work. The Windows DLL containing this new A-R
model is posted on CompuServe and Internet. Those wishing to use
the new model may download the DLL for FREE. This represents a
good example of how easy it is to add new models to ISSPICE4.
The DLL approach contrasts the update path used by other vendors
which can take months and require major software updates.
Figure 2, and the figure below, describe a second
order IIR low-pass filter. The starting point in the design process
begins with
the continuous transfer function in the Laplace domain:
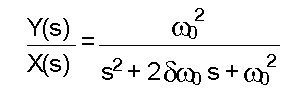
Using the trapezoidal rule, the Laplacian operator, s, may be replaced by
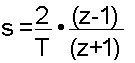
and the continuous transfer function
may be transformed to the discontinuous, canonical one:
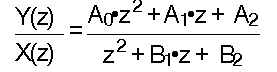
Setting the damping coefficient to d=0.25, the cutoff frequency
to wo/2þ=1 kHz, and the sampling period to T=100 µs,
one obtains the transfer function:
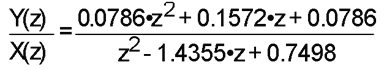
Both the impulse and step response of this system are derived
in [4] and are confirmed with the ISSPICE4 simulation shown in
Figure 3. Note the transmission line based
delay and Laplace expressions can both be used in the AC and transient
analy- ses, whereas the event driven model only works in the time
domain.
An application for FIR filters is the enhancement of signals buried in noise. When signal and noise are covering different bands of frequency, separation with conventional recursive filters is possible. However, when both spectral ranges are overlapping, selection has to be made by other methods.
Generally, signals differ from noise by their periodic behavior and their inherent redundancy. Noise, on the other hand, is random and stochastic. As an example, one should imagine a noisy television test image travelling from a transmitter to a receiver over great distances. Increasing the gain doesn’t enhance quality because the signal and noise are both emphasized, leaving the signal-to-noise ratio unchanged. Yet, when the video image is exposed to the light sensitive film of a camera for a fairly long period of time, a significant improvement in quality may be observed. The quality is further improved with the time of the exposure.
The bright and dark parts of a video image that form the test pattern appear at the same position on the film, exposing it more intensively than the noise with every new picture. This process is called signal averaging and leads to an improvement in the signal-to-noise ratio that is proportional to the square root of the number of repetitions. However, this process is only valid if the information content during the integration period isn’t subjected to considerable changes. The transfer rate and integration period are antagonists and have to be harmonized.
It is very important to know the period of the signal frequency which has to be detected in the noise. With a high number of repetitions, the averager becomes very narrow banded and the pass band has to be tuned accurately to the signal frequencies of interest. Waveforms of signals remain preserved because harmonics coincide with the comblike pass bands. Sidebands, noise and other frequencies, which are not at integer multiples of the signal frequency will be suppressed.
he circuit in Figure 4 demonstrates
the enhancement of a signal buried in noise. A FIR filter with
9 sections and Dirichlet weighting is used. The input signal is
created by adding an ISSPICE4 time domain noise generator, with
500mv RMS noise signal, to a 1Vp-p sine wave. The sampling period,
T, is exactly tuned to the known period of the signal (1 Hz).
Therefore, all the sine waves appearing at the taps are equal
in phase and summed up linearly with the number of sections. Random
variations, on the other hand, are alternately positive or negative,
thus growing only with square root of the number of summations.
The summation occurs by connecting the output
of each delay element together. Figure 5
shows the results. While this simulation could be performed with
analog elements, the event driven algorithm (68.96s) is 50% faster
than the standard SPICE matrix solution algorithm (103.43s).
The ability to mix digital elements like state machines, sampled-data elements like FIR and IIR filters, and analog circuitry is unique to Intusoft’s implementation of SPICE. It offers superior capability over dedicated DSP software and other competitive products which are limited in their ability to mix signal domains.
References
[1] “Electronic Filter Design Handbook”, A. Williams,
McGraw-Hill, 1981, Chapter 11
[2] “Digital Filters: Analysis and Design”, A. Antoniou, McGraw-Hill, 1979
[3] “Digital Signal Processing”, A. Oppenheim, R. Schafer, Prentice-Hall, 1975
[4] “A SPICE Cookbook”, K. Muller, Intusoft, 1991
|
|
|
|
Current Price |
New Price (as of 8/4/95) |
| ISSPICE1.5MNC | All Macs/Power Mac | 2G.6 | $95 | $95 |
| ISSPICE3 | All Macs/Power Mac | 3F.2 | $795 | $990 |
| ICAP/4M | All Macintoshs | 3F.2 | $1750 | $2240 |
| ICAP/4PM | Power Mac only | 3F.2 | $1750 | $2240 |
| ICAP/4Macintosh | All Macintoshs | 3F.2 | $2595 | $3300 |
At DAC Intusoft will unveil a new multithreaded, multiprocessor version of ISSPICE4 running under Windows NT. The main portions of the Newton-Raphson algorithm, namely, the model evaluation and load, and sparse-matrix solution have been parallelized in this new version of ISSPICE4. This allows the SPICE simulation speed to nearly double simply by adding another processor.
The simulator starts by partitioning the circuit in a binary tree structure. The depth of the tree can be selected based on the number of available processors. The circuit is partitioned based on our proprietary iterative mincut heuristic algorithm.
There are three basic analysis types in SPICE: AC, DC, and transient. AC analysis is the easiest to parallelize since the solution at each frequency is independent. By contrast DC and transient analyses are iterative processes repeatedly performing the following steps until convergence is achieved:
LOAD: In this step the device model equations are evaluated and the circuit jacobian matrix is updated to setup a non-symmetric sparse system of linear equations.
SOLVE: In this step the equations from the previous step are solved using a sparse LU decomposition followed by forward
and backward substitution.
It is not unusual for the above steps to take up to 90% of the total simulation time. Intusoft has developed a proprietary algorithm that parallelizes the execution of these two steps at each iteration resulting in a significant (linear) decrease in the simulation time.
Each Newton-Raphson iteration is divided into tasks which are
executed serially or concurrently. Those tasks that are performed
serially are said to be in a single thread phase and the ones
that are executed concurrently are said to be in a multithread
phase. In a multiprocessor environment, each process in a multithread
phase can be dynamically assigned to a processor by the operating
system (in this case Windows NT). The operating system also provides
the necessary event flags used for the synchroni- zation between
processes. The LOAD and SOLVE steps at each iteration are executed
in a multithread phase. In addition, at each iteration entire
subcircuits resulting from the circuit partitioning) can be declared
latent. Such subcircuits do not have to be processed for subsequent
iterations until the latency criteria is no longer satisfied.
This means that even in a single thread environ- ment (Windows
95) our implementation will identify these latent subcircuits
and save a significant amount of LOAD time per iteration.
BACK
TO THE TOP
Current mode design techniques are not new, but the development of high performance complementary bipolar processes with excellent matching properties has allowed current mode principles to be fully exploited. The emergence of monolithic devices has led to a renewed awakening of the benefits of current mode design and produced a wealth of circuits with broadband properties [1].
The current conveyor (CC) was first introduced by Smith and Sedra [2, 3] and has proven to be a versatile analog building block. It can perform many familiar signal processing functions with new levels of performance for detector, converter, rectifier, filter and amplifier designs.
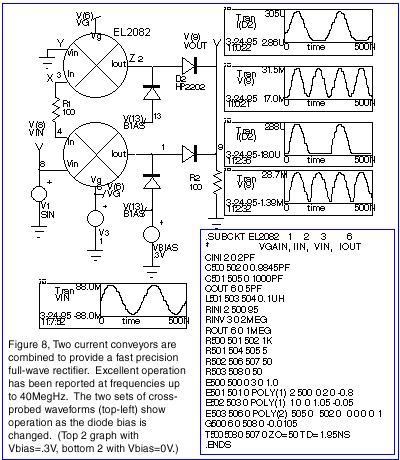
The basic structure (Figure 7) of a CC is simply a voltage-mode op-amp with output current-mirrors. The CC comprises a low impedance current-input/voltage-output (X), a high impedance voltage input (Y) and current output (Z). The port relationships of the conveyor are: Vx=Vy, Iy³0 and Iz=Ix. The CC has precise unity current gain between X and Z, rather than the poorly defined high open-loop gain of the voltage op-amp. The advantage is that the closed-loop gain-bandwidth conflict of negative feedback voltage-mode op-amp circuits is avoided.
CC circuits can also be implemented using off-the-shelf voltage-mode op-amps in a variety of configurations [1, 4, 5]. High precision is obtained using a floating structure, while wide bandwidths and high slew rate are obtained using supply current sensing techniques. With this technique you could indeed build a cheap CC using a µa741 up to its nominal unity gain bandwidth! Examination of the architecture of a current-feedback op-amp (Figure 7) reveals that the basic CC structure is used internally. In implementing a current-feedback op-amp, hardware vendors have disguised the CC in favor of a topology more familiar to voltage-mode op-amp users. Only recently has the CC appeared independently in a monolithic device making it truly useful in many designs. [10, 11]
Rectification of low-level signals is an important aspect of signal processing. The traditional approach using diodes and op-amps can encounter distortion during the zero-crossing due to the op-amp’s finite small-signal dV/dt behavior. This fact limits high frequency operation. Various schemes have been reported using the CC configured as a differential V-to-I converter followed by pre-biased diode rectification to produce significant performance improvements [6, 7, 8]. Applying a bias to the bridge aids performance by reducing the maximum dynamic impedance of the bridge at crossover.
Figure 8 shows a precision full-wave rectifier using 2 CCs. The CC is modeled using the élantec 2082 current mode multiplier macromodel [11]. Another alternative would be to use a current-feedback op-amp macromodel, such as the 2260, without the output stage, since the core of a current-feedback op-amp is a CC. All of the new models in the élantec data book are compatible with ISSPICE4 and are included on the newsletter floppy disk for subscribers.
The ISSPICE4 simulator allows you to easily sweep circuit and
model values. In this case, after setting up the rectifier circuit,
VBIAS was interactively swept to find its effect. Figure
8 shows waveforms from two VBIAS settings, 0V and 0.3V, at
a frequency of 4MegHz. The results show excellent correlation
with measured data [3, 4]. Different models and key device parameters
were also explored with simulations at 30MegHz revealing strong
diode related sensitivities. It was found that Schottky diodes
with low CJO and recovery time (i.e. BAT85, BAT81, HP2817, HP2202,
and HP2280) work best. Although Schottky diodes offer the best
speed advantages diode-
connected complementary transistors (like the EN2016/EP2015) can
offer a cheaper alternative, especially in a monolithic implementation.
The current conveyor is new to the marketplace so many applications have not been explored. In future newsletter articles we will investigate other current mode designs and how interactive simulation can help you tackle them.
Author’s Note: The author wishes to thank Gerson
Machado for his invaluable efforts in this and other newsletter
articles.
“Mixed-Environment” Simulations
It is clear that the functionality provided transitions ISSPICE4 from a circuit simulator into a mixed environment (hardware/software) simulator capable of tackling system level designs that other simulators can’t.
Schematically, the APCML objects connect like any other electronic
device. Input and output objects convert between
real world hardware, or data stored in files, with either traditional
SPICE elements or high level algorithms. For example, you will
be able to stimulate your design with sound from a file, or microphone,
as shown in Figure 1. The sound can then
be compressed and processed by traditional analog or digital circuitry,
or by an algorithm such as an FFT or wavelet transform. Using
the interactive capability of ISSPICE4 you will be able to study
both electronic and algorithmic variations. In Figure
1 the compression ratio is swept to hear how the output sound
changes. Note that part of the compressed data stream is simulated
with traditional SPICE simulation algorithms. It is then recombined
before output to the speaker. Connection to the underlying analog
simulator allows the user to push down into the details of a design
hierarchy in order to compare the detailed implementation with
a more abstract system view.
The APCML provides source code and OLE 2.0 in-process server
DLL’s for a number of functions (Figure
6). Each of the
APCML objects can have methods needed by other applications. For
example, you could add an interface to render a pictorial or graphical
view for a schematic capture application. Intusoft will add some
of these interfaces in the forthcoming release of an OLE2 compatible
ICAP/4 system. The interconnection between ISSPICE4 and the OLE
2.0 objects are provided by the APCML DLL. You can add your own
array objects by using a C++ compiler capable of building OLE
2.0 32 bit in-process server DLL’s. The source code for the
servers, included with the APCML, is provided so that you can
develop your own servers. Most array processing extensions can
be made using the APCML, however, the CMSDK is required to extend
the functionality of APCML DLL. It should be noted that
the APCML object were created with the CMSDK.
|
Wavelet Transforms:
Variable Radix FFTs:
Matrix Math - non-sparse:
Input:
Output:
Figure 6, The list of new models in the Array Processing Library. Schematic symbols allow each function to be graphically interconnected. |
The Code Model Software Development Kit, or CMSDK, allows you
to develop analog and mixed signal HDL models using C
code subroutines. The Intusoft HDL differs from competitive offerings
which are proprietary and only work with UNIX based
simulators. With the kit you can greatly expand the functionality
of ISSPICE4 by adding your own models and functions.
What’s Included in the CMSDK and Special Pricing
The CMSDK consists of a compiler and other tools, code model
examples and source, include files, and documentation on how
to create HDL models. The toolkit is supported under Microsoft
Visual C++ 1.1 or 2.x under Windows NT or Windows95. While
models must be developed under NT or Windows95, they can be used
with ISSPICE4 under any Windows (3.1x) version.
The limited time offer originally due to end April 15 has been
extended to June 15, 1995. The price of the CMSDK is $2500.
After 6/15/95 the list price will be $3500.
Copyright ©2002 Intusoft, All Rights Reserved