|
|
|
|
|
|
|
In Spice, capacitors are modeled as ideal parts with
no losses or inductance. When more detail is needed, we generally add
a series resistance and perhaps some lead inductance. Follow this link
to find out more: But, is that enough? If you look at manufacturers data
sheets, youíll find a specification for Dissipation Factor (DF). Tan
delta is about the same thing (DF = real(z)/Im(z) vs. |
|
||||||||||||||||||||||
|
In researching this, we
came across an article written by Bob Pease on "Capacitor Soakage"
http://www.national.com/rap/Application/0,1570,28,00.html.
In this paper, Pease outlines the historical problem with capacitors remembering
their previous charge by recovering some of the original charge after
a brief discharge. This was originally recognized as a low frequency problem,
plaguing circuits using certain capacitor dielectric materials for integrators.
Later, the widespread need for sample and hold circuits for digital interfaces
caused the problem to be revisited for higher frequencies. In his paper,
Pease showed how most capacitors scaled with time such that the soakage
error increased as the time scale increased. Could this be modeled using
a constant DF? |
||||||||||||||||||||||
Work done by John Prymak at Kemet confirms
this behavior. Intusoft first published Prymakís model in 1995. See http://www.intusoft.com/nl44.htm#modeling.
These models have been updated and applied to the Kemet line
of capacitors using the software download at: http://www.kemet.com/KEMET/web/homepage/kechome.nsf/vabypagename/spicesoft, which gives plots of ESR and impedance magnitude vs. frequency. |
|||||||||||||||||||||||
|
Now returning to our original problem of modeling capacitors. Given the frequency domain response, can we make a lumped equivalent circuit that accounts for the frequency domain data. If it uses the topology shown by Bob Pease, will it agree with the published data? Hereís the circuit offered by Pease for a Mylar dielectric:
After playing around with this circuit, we came to the following conclusions:
Our objective here is to model ceramic capacitors that are shown to have constant DF over a wide frequency range; hence the geometrically increasing time constants. The model was applied to a sample and hold circuit
using a high k ceramic capacitor. Poor performance resulted. Sure enough,
the voltage drooped excessively and remarkably, the accuracy was proportional
to the DF, shown in Figure 2. Remember, DF is mostly given at 60Hz,
so we can predict how well our high-speed circuits work based on low
frequency 60Hz measurements!
Figure 2. Plot of Magnitude (magz) as Real (rez) versus Frequency for Mylar Dielectric Circuit. Our model used 6 R-C and 4 L-C sections. This appears to be overkill for the description of a second order effect. Probably the biggest impact of the model will be in power filters that work below the capacitor resonance or filters that may be used in the telephone frequency range. That would narrow our frequency range to the 10Hz to 10MegHz range. Thatís 6 decades, which would suggest using 6 sections and stepping the time constant geometrically by 0.1 for each section. However, resonance for some ceramic capacitors is in the 100 MegHz range, so we need an extra R-C section for these devices. Weíll leave one L-C section for power filters that are used above resonance and 6 R-C sections for the lower frequency model. Our model inputs will be:
Weíll assume DF above resonance is the same as DF below resonance. The model is shown in Figure 3 for these inputs:
Figure 4. Plot of Magnitude (magz) and Real(rez) versus Frequency. Now, with our new model, letís explore some common circuits to see the impact of a more accurate model. The circuits weíll try are:
The sample and hold circuit shown in Figure 5 was used to measure soakage error vs. DF. When the sample and hold is used as part of a data acquisition system, it manifests itself as cross talk. The capacitor voltage changes during the hold period, moving toward the previously sampled value. When the previously sampled voltage is less than the current sample, it looks like a droop or a sagging voltage; however, the results of applying a triangular input waveform in Figures 6 and 7 reveal its true nature. Moreover, changing the capacitor value has little effect on the error. The error tends to be proportional to DF and is very large for X7R ceramic capacitors.
Figure 5. Sample and Hold Circuit.
Figure 6. The output moves lower toward the previous sample.
Figure
7. The output moves higher toward the previous sample. The notch filter shown in Figure 8 is a parallel filter that produces zeros of transmission when the signal taking the two circuit paths are equal and 180 degrees out of phase. If ideal components are used, the resistor and capacitor ratios shown will produce infinite attenuation. To analyze this circuit using pencil and paper, calculate the y21 and y22 for each section and add them together to calculate the overall transfer function -- vout/vin = -y21/y22 See http://www.intusoft.com/nl62.htm#2portcharacter to use simulation to do the same thing. Variations of this circuit are commonly used to eliminate the 60Hz hum in audio equipment.
Ceramic capacitors are relatively inexpensive and small so that they become a first choice based on size and economy. Figure 9 shows how the notch frequency and attenuation vary with DF. At the very least, you will have to account for DF in selecting component values if you choose to use ceramic capacitors.
Figure 9. High DF capacitors change notch characteristics. Finally we looked at the unloaded filter section of a Voltage Regulator Module (VRM). This is typical of a circuit used to supply power to a microprocessor. The parallel ceramic capacitors are located very close to the microprocessor, with some on the chip itself. The reason for this is the ability of the chip to change its load in just a few nanoseconds from low to high power. With a 1nH interconnect, this requires 100 volts to control 100 amps in 1 nanosecond. This is beyond the capability of power supply technology so that itís necessary to absorb these changes in load using capacitors mounted close to the chip. Figure 10 compares models with and without soakage. The switching frequency would typically be in the low mHz region.
Figure 11. Comparison of conventional model (gain2, phase2) and Soakage model (gain, phase).
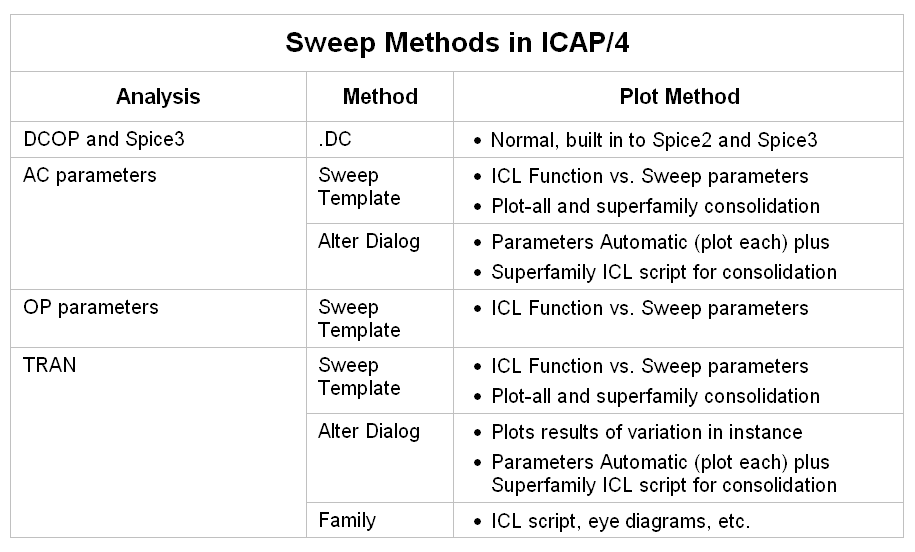
There are several ways to conduct parameter sweeping in ICAP/4. We can sweep families using the DC operating point (DCOP) capability originating in Spice2, the Alter dialog from SpiceNet, or by using the SWEEP template. Still, thatís not enough. If you were to build a curve tracer in a transient analysis, then you would step the outer parameter as a function of time. That would create one long plot while you want the x-axis to retrace every time the outer parameter steps. This is the same problem that must be solved to produce an "eye" diagram. In each case we need an x-axis vector that resets to its starting point at regular time intervals. When Scope5 sees the x-axis vector returning to its starting point, it assumes that you are plotting a family and it blanks the re-trace line. There are several ways to solve this problem. One way is to make a new vector with the same length as the default vector and then walk through the default vector copying it into the new vector. Whenever we reach a retrace point, subtract a sumtime scalar from all subsequent points, where sumtime = sumtime + timestep. A better approach is to use the mod (%) operator. This operator applies to integers so we need to make a new vector that is an integer with sufficient precision to satisfy our accuracy needs. Then we convert it using the mod operator. In this case we donít have to walk through each point, the ICL does it for us, which is much faster. The speed gain occurs because the ICL parser does the vector arithmetic for you within a C language for-next loop. Hereís the function weíll use:
The time vector is scaled so that its last point becomes 1e9 to satisfy the integer requirements. After performing the mod operation, the original scaling is restored. This gets us an accuracy of 1 part per billion, which should be sufficient! Remember that the ICL turns the "default" and "current" vector names into aliases for the x-axis and the currently selected vector. Putting it together, this is the full script:
If you destroy the original plot, your graph looks
cleaner; however, leaving it around lets you link the 2 plots and use
parametric cursors to walk through the family plots data.
Figure 12. Superfamily ICL
script collects all data into a single vector with a sawtooth x-axis. Figure 12 shows how this works to make an "eye" diagram. This eye diagram is used to evaluate a filter used in spread spectrum communication. A pseudo random noise signal was the input. The filter is used to limit the frequency spectrum. The filter dispersion causes the temporal spreading of the "eye." Dispersion is due to the phase delay. d(phase)/d(frequency) is not constant. You can inscribe a rectangle inside the eye to define acceptable logical thresholds along with setup and hold times. Another kind of sweep occurs when a large number of transient data runs are plotted using the Alter dialog or the plot-all button in Scope5ís Sweep dialog. For these cases, viewing an overall envelope is more desirable than plotting each waveform separately. To do this, we made an ICL script called superfamily that collects everything in a plot into a single vector with a sawtooth x-axis.
Figures 13a and 13b illustrate the use of a superfamily plot taken from a simple B-element expression.
Figure 13a. The result of doing a "plot-all" from Scope5ís Sweep dialog. You can see that plot-all gives access to each case;
however, the presentation is cluttered. After running the superfamily
script, an uncluttered presentation results, as shown in Figure 13b.
To summarize, all of the sweep methods available in ICAP/4 are listed
below.
|
||||||||||||||||||||||||||||||||||||||||||||||