| Newsletter List | |
|
|
Hysteretic Average Model |
|
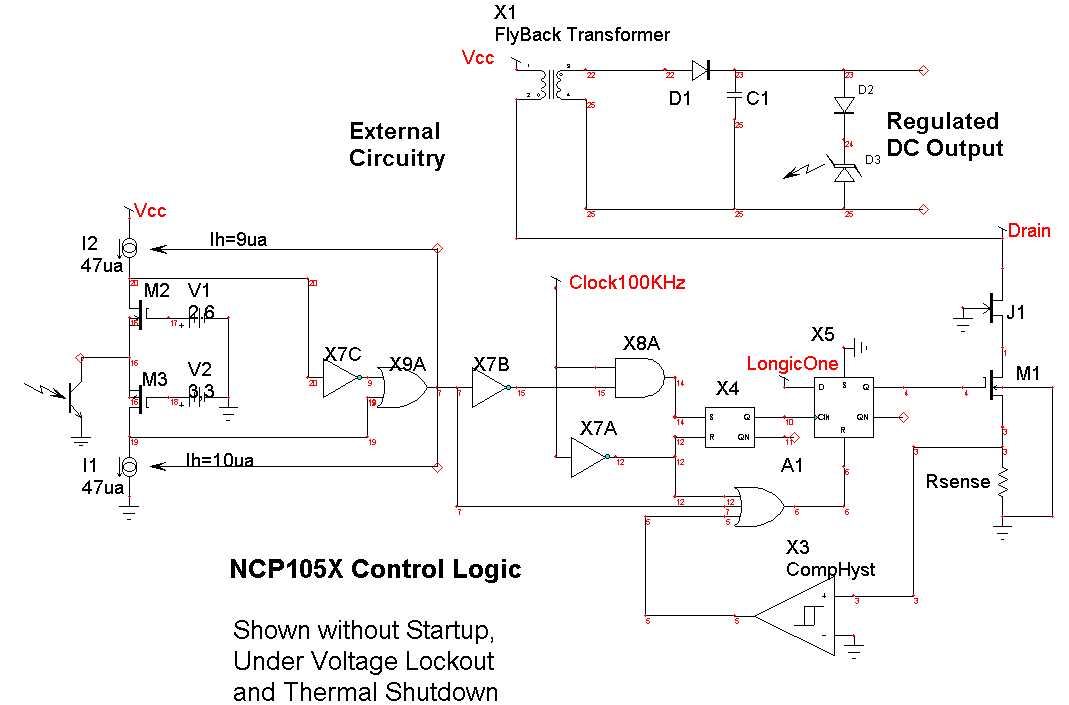
Average models are used to construct a continuous time model for switched mode power supplies, SMPS. They offer the advantage of very fast simulation times and provide a linear circuit representation for doing an AC analysis. The AC analysis allows a designer to observe the loop gain and adjust compensation components to get acceptable gain and phase margins. The hysteretic power supply using an NCP1050 series IC has essentially 2 control loops. The inner loop causes the Flyback charging current to be limited using current feedback. The block diagram shown in Figure 1 shows the control loop logic. |
|
||||||||||
 |
|
The drain current pulse is formed by charging the Flyback inductance until the voltage across Rsense reaches a fixed threshold. When that occurs, the PWM switch is turned off. The PWM is held off until the next clock pulse after the output voltage drops below the set point. This loop operates in discontinuous conduction mode so that the output and input currents are given by D*.5*L*Imax^2*F/Vout and D*.5*L*Imax^2*F/Vin respectively. For a constant input voltage and load current, the PWM on time is fixed and the duty ratio is controlled by the OFF time. The self-oscillating frequency exhibits some subharmonic oscillation because the internal oscillator synchronizes the turn-on, which is 100KHz for the device shown. To make an average model for the self-oscillating section we must assign a control loop gain that makes this section stable and accounts for the oscillation using Z-Transform derived difference equations. The reason for describing the self-oscillating section as a stable circuit derives from the concept that a system that is oscillating has increased losses that damp the oscillation, forming a stable limit cycle. We observe that the duty ratio of the hysteretic converter can go from 0 to 1 as the control signal traverses the hysteresis band. That suggests that we set the duty ratio to the linear control signal at the output of the opto-coupler divided by the hysteresis width. We would expect to get zero gain margin for that condition. For the average model to be useful, it shouldn’t oscillate so that we divide the control signal by 1.5 times the hysteresis to get about 3 dB gain margin. Figure 2 compares the switching result with the average model for a load switch from 20 Ohms to 4 Ohms at 6ms into the simulation. Bode plots for different loads reveal about the same gain and phase margin with the critical frequency running about .5 times the limit cycle frequency. For a load of 20 Ohms, the frequency for 0dB gain was 26kHz and the switching frequency was 45.4kHz, as shown in Figure 3. |
|||||
|
A new Spice element was needed to account for the variation in switching frequency with load. To accomplish this, a code model was made with a variable delay time connected to an input port. In the time domain, it’s just a delay, outputting the historical data according to the requested delay. In the frequency domain, it’s an e^-sT function (Z^-1). It’s combined with a continuous Laplace integrator using a subcircuit model to make a fraction order hold, FOH [1], that works in both the frequency domain and the time domain. The FOH is a generalized model that can be used to simulate a Zero order hold (k=0) on up through a first order hold (k=1) and anything in between. We used k=0 for this model. By properly accounting for large signal dependencies in the difference equations, this “average” model is also a large signal model capable of studying turn-on, line and load steps and other large signal behavior. The improved simulation speed enables us to use the ICAP/4 optimizer to center the design, getting the best performance by selecting just the right component values. With the following definitions, we can develop equations that describe the average model:
The equations we need are then:
But IC is known because the charging inductor is running in discontinuous conduction, dumping ½*LP*Ipk^2*F power; so that:
And IL can be measured so that TD can be computed. |
|||||
|
Discussion of Use and Limitations The actual circuit cannot have an exactly correct duty ratio for each cycle because of the 100kHz clock synchronizing. The duty ratio wanders around the correct result, producing subharmonic content and a more accurate average value over longer time intervals. This behavior is not expected to produce serious errors, especially in determining stability margins with respect to filter and load characteristics. The discontinuous conduction assumption is violated during start-up, so that it is necessary to add mode-switching logic. We’ll do that in a later 8.x.11 software release along with time domain validation of the “average” model using new GFT software techniques. See the article “2003 Brings New Software Updates, Server License and Macintosh Product” on pg. 13 of this newsletter. Or watch our product preview at the Applied Power Electronics Conference, February 9-13, 2003 in Miami. The NCP105XA model delivered with the ICAP/4 software is shown in Figure 4 and its use is illustrated in Figure 5. In its initial release the under voltage lockout and short circuit protection is not included. The new FOHvar model needs the updated cml.lib, power.dll and updated symbol libraries. All are available to registered users with current maintenance from Intusoft at http://www.intusoft.com/support.htm To use the average model, you need to place power.dll into <IcapsDir>\is\power.dll. Library onicavg.lib contains a model for the NCP105X power converter called NCP105XA and its symbol is in ONICAVG.sym. Models vardelay and FOLvar are in cml.lib use power.dll to account for the changing frequency with operating point. |
|||||
|
Figure 4. An average model for the NCP1050 series Switching Regulator. Figure 5. Using the NCP1050 series Switching Regulator average model. |
|||||
New Spice Convergence Aid |
|
There are certain cases for which DC convergence fails
because of singularities in the DC operating point. A zero order hold
is an example that cascades a z transform differentiator with a Laplace
integrator. The resultant product of 0 times infinity produces a non-convergent
DC result; however, an AC crossover network eliminates the problem node
so that it is fair to remove it from the convergence test. R3 and C1 shown
in Figure 6 bypasses the DC solution that otherwise
cascades S-plane integration with Z domain differentiation.
|
|||||||||||||||||||
|
Increasing VNTOL can remove the non convergent behavior;
however, VNTOL is global and increasing it to solve the problem at one
node will reduce the DC operating point accuracy. If the user were to
manually enter VNTOL for each node, the bookkeeping management would become
difficult. Intusoft has introduced a new IsSpice option, AUTOTOL. An array
of values holding vntol[ ] and abstol[ ] for each node and source current
is initialized with the VNTOL and ABSTOL values. If AUTOTOL is set larger
than 1, then when a node or branch current fails to converge, its tolerance
value is multiplied by AUTOTOL. Setting AUTOTOL=2 will rapidly eliminate
offending nodes. Smaller values will make the elimination occur more slowly
and have a less sever affect. If AUTOTOL is set to less than -1, the same
thing occurs using the absolute value of AUTOTOL and the “.OUT” file reports
the activity so that you can isolate problem nodes and sources. AUTOTOL
is only active for the initial DC operating point calculation. To use
the AUTOTOL option; enter .options AUTOTOL = [value] in the user statements
field of the IsSpice4 simulation setup dialog. |
|||||||||||||||||||
Nulling Techniques
Aid
|
|||||||||||||||||||
|
Back in March 2001, Newsletter 62 illustrated IsSpice techniques for measuring Two-Port network parameters for various sets of network equations. The very last topology was the transmission or T parameters. To evaluate these T parameters, a SPICE3 behavioral element was used to adjust the voltage at one port so that the open circuit voltage at the opposite port becomes unity. We didn’t explain why this should work and as it turns out the use of this technique is also central to application of the Extra Element Theorem [2] using a SPICE simulator. In the lab, adjusting in-phase and quadrature signals to achieve the desired result does this. All that’s necessary is the presence of a network to transmit the signals from the injection point. But is the technique valid using the AC Analysis of a SPICE simulator? The AC analysis feature of SPICE simulators, including IsSpice4 from Intusoft, operates as follows: |
|||||||||||||||||||
|
|||||||||||||||||||
|
Limitation of AC Analysis The underlying idea is to linearize the circuit about its operating point to get a small signal equivalent circuit and its transfer function. Modern SPICE simulators, including IsSpice4, include arbitrary sources in their SPICE primitives. The arbitrary sources include a wide range of nonlinear behavior; including multiply, divide, transcendental functions and if-then-else switches. Each of these mathematical functions is set to return derivatives so that the AC matrix can be formed. Multiplication can be used to study the behavior of the other nonlinearities since for the most part all of the others can be equated to a polynomial series in which only multiplication is involved. The basic assumption of a small signal model is that nonlinearities have vanishingly small effect as the signal level approaches zero. In the case of multiplication; the IsSpice4 derivative calculation is done as follows: d(UV) = UdV + VdU = Uv + Vu Where the upper case denotes the DC value and the lower
case is the small signal value of the input signals. If the input signals
were at a single frequency, f, with some variable phase, then the output
would consist of a DC component a complex signal at f and another complex
signal at 2f. You can see that the above derivative calculation correctly
accounts for the behavior at f and discards the DC and 2f components.
That’s where the underlying assumption is vulnerable, because further
nonlinearities would couple energy back into the signal at frequency,
f, if the discarded components were evaluated. This result invalidates
the AC analysis for phase locked loops and mixers; however, no unwanted
components are created for scalar multiplication. The injection of a high
gain signal to achieve a desired result is similar to using an operational
amplifier to reduce and error signal to an acceptably small value. Moreover,
there is no need to iterate the AC matrix since a solution is guaranteed
if a non-singular network exists that has a finite signal transmission
from the injection point to the desired set point. Now we can turn our attention to the notion of what acceptably small means and how much gain should be used. As the gain is increased, then the error signal that is being nulled is reduced. Both numbers must exist as 64 bit floating-point numbers. Suppose we have a simple network of resistors as shown in Figure 7a. The corresponding figures are described in Figure 7b. Figure 7a. A simple null generator and the MNA equations.
Figure 7b. The null generator MNA equations. Then we add one more element with an equation to null v2: This is the same as placing an amplifier between v2 and
v3 and has the same consequence. The precision of v2 and v3 depend upon
evaluating the equation, gain*v2-v3 = 0 When this is plugged into the IsSpice4 simulator, the correct answer is given even when the null gain exceeding 10e30. In circuits with complex transfer functions, problems with phase and gain accuracy begin to occur near the 64bit precision limit. This occurs for null gains as low as 1e13. The errors are mostly associated with representing quantities that mathematically approach zero or infinity; resulting in large phase errors. Notice that for AC analysis, the gain polarity doesn’t matter. A null can be calculated even with positive feedback. Loop Gain Revisited We have discussed the use of signal injection to measure “loop gain” and thereby predict stability margins. A widely used technique was described in Intusoft’s September 1999 Newsletter, NL57, page 10.
Using this technique requires the insertion of a series voltage source that is used to excite the loop. But if the voltage source is placed in series with a current generator, for example, the collector of a BJT; then, it will not excite the circuit and the technique fails. For that case, the current gain should have been measured and the circuit excited with a current source. But what if the loop can’t be broken at a current source or a voltage source? If you look at the Hysteretic converter, which is described on Page 1 and shown below in Figure 8, you’ll not find a decent place to break the loop for a transient simulation. About the only place is inside of the ripple filter. The signal at the collector of the opto-isolater is a switching signal and can’t be used for hardware measurements. And the feedback loop includes signal flow through both R15 and R7. While either a voltage or current source provides excitation, the resulting transfer function doesn’t agree with one placed inside of the average model. That dooms hardware verification of the “loop gain” unless we can find a way to account for both forward and reverse current and voltage gain. It turns out the application of Dr. Middlebrook’s Extra Element Theorem [2], EET, can solve the problem by making measurements using null injection that we also discussed earlier. We explore this problem in our next newsletter and demonstrate the technique at the Applied Power Electronics Conference (APEC 2003) this February in Miami Beach, Florida.
Figure 8. The loop cut shown between R4 and
L1 is neither a voltage nor current driven injection point. |
|||||||||||||||||||
2003 Brings New Updates,
|
|||||||||||||||||||
|
New Usability Enhancements Intusoft is set to release on February 17, Version 8.x.10, Build 1989, of the ICAP/4Windows family of software. A preview will be shown the week before at APEC in Miami Beach. This preview will cover things like:
Figure 9. Expand and rescale by setting the cursors to 990u and 1 m; then press x to expand the x-axis scale and press t to tile the expanded region. |
|||||||||||||||||||
|
Web and Client-Server Networking Ordinarily, IsSpice runs on the users workstation, even
when a network license is purchased. To facilitate web-based services,
Intusoft has now made available a version of its ICAP/4 package that is
licensed to run remotely on a server. The software includes Icaps.exe,
Spice4.exe and associated libraries. Typical use of such a package is
to run canned topologies with minor variations that showcase third party
products. For this usage to make sense, problems must be small so that
latency will be acceptable. (Latency is the time elapsed between a request
for web service and the returned data.). Licenses are issued for 1,2,3
and 4 processors per server machine. The software is available for Windows
NT and XP. The licenses are sold per processor and are time locked for
one year at a time. Two pricing models are available. First, you can purchase
the software under our current agreement and keep it active with an annual
fee (about 15% per year). Secondly, you can purchase an annual license
only. The second option is considerably less expensive for the first year;
however, by year 4 it costs more. The advantage is that you can choose
to add more licenses at any time so you can easily balance your web service
with customer demand. The Mac is Back! ICAP/4 can now be run on the Apple Macintosh Computers by using Connetix Virtual PC 6.0. Try it out on the demo that’s on our web site. Be sure to order the Mac version, it uses a virtual key instead of a hardware dongle. Intusoft first developed for the Macintosh in September of 1989. [1] Benjamin C. Kuo, 1963, Analysis and Synthesis of Sampled Data Control Systems, pg 49-51. [2] R.D. Middlebrook, V. Voperian and J. Liu, IEEE Transactions on Circuits and Systems, September 1998, The N Extra Element Theorem
|