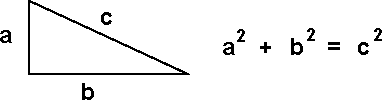Turns Counter Project

An electronic circuit will be constructed using the ICAP/4 package that counts the turns of a rotating shaft. Counting shaft revolutions is a common problem. From a car odometer to a model robot, the problem is frequented in many real-world instances.

This project requires a basic knowledge of algebra. It will also use elements of trigonometry, calculus and Boolean algebra that will be explained if you haven't been exposed to these subjects. If you are familiar with these topics, simply skip ahead to the Encoder Model.

Pythagorean Theorem
Dating back to circa 1900-1600 B.C., the theorem was discovered on a Babylonian tablet. The theorem defines the relationship between the sides of a right triangle and its hypotenuse.

Figure 1: The Pythagorean Theorem was known for more than 1000 years before a formal proof was documented.

Later Pythagoras, or someone from his school circa 560-480B.C., may have made the first known proof, and the theorem bears his name. Today, there are many proofs; the following is one of the simplest:

First, arrange 4 identical right triangles as shown in cyan to make a square inscribed within a square. The area of the larger square can be calculated two ways. A=(a+b)*(a+b), or by summing the inner square area (c*c), and the triangle areas (4*b*a/2). Then A=a2+b2+2ab = c2 + 2ab, and finally a2+b2= c2.

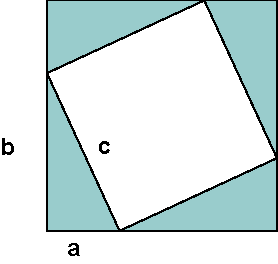
Figure 2: Arrange 4 identical triangles as shown, then calculate the outer square area 2 ways: (a+b)2 = 4ab/2 + c2.

Circles and sine waves

The sine and cosine functions can be derived using the Pythagorean Theorem.


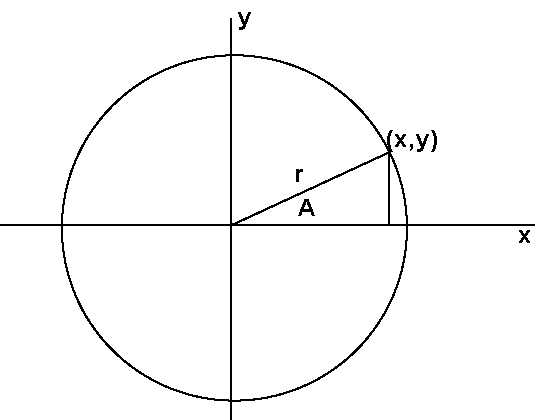
Figure 3: If r is constant, a circle is defined and the Pythagorean Theorem defines the (x,y) points that lie on a circle.

With the geometrical definition in figure 1, use the Pythagorean Theorem to define the following functions:

sin(A) = y/r = y/sqrt(x^2 + y^2)
cos(A) = x/r = x/sqrt(x^2 + y^2)

If the circle represents a shaft cross-section, then as the shaft rotates, A will change. You can find x and y as follows:
y = r * sin(A)
x = r * cos(A)

Enter pi

It was recognized early on that the ratio of a circle's circumference to its diameter is a constant, no matter what the circle's diameter. We now call that constant pi. Around 2000 B.C., the Egyptians found it to be about (16/9)2 (.6% error), about the same time the Babylonians settled on 3+1/8 (.5% error). Circa 550 B.C, some argue the Bible references pi as 3 (4.5% error). Then Archimedes of Syracuse (287-212 B.B.) was the first to establish a method using polygons that can compute pi to any given accuracy, he calculated pi = 22/7 (.04% error) using 96 sides. Later, Zu Chongzhi from China (430-501) used a polygon method to compute pi to an accuracy of about one part per million. Now, with modern computers, pi has been calculated out to 1,241,100,000,000 digits. We need to know about pi to change rotational speed that we will simulate using ICAP/4 in revolutions per minute (RPM), into an angle that changes with time.

First, a definition of the angular unit is needed. Degrees are used in everyday conversation, however, as a dimensionless quantity, the radian makes more sense in mathematics and engineering. Specifically, an angle A sweeps out a segment of a circle. The segment length (s) is given by s = r*A. Then A = s/r radians. When s=C, A=2*pi, so there are 2*pi radians in a circle or:

2*pi radians = 360 degrees.

Finally RPM is converted to radians/second as follows:

Angular speed=RPM * 2*pi radians/revolution*60Second/minute*time = pi/30*RPM rad/sec

Next, the angle must be computed. For constant RPM, just multiply by time. However, if RPM is allowed to vary with time, we need to sum each RPM*dt, where dt is an arbitrarily small time interval, as shown in Figure 4 . As the time interval dt approaches 0, the function is defined as the integral.
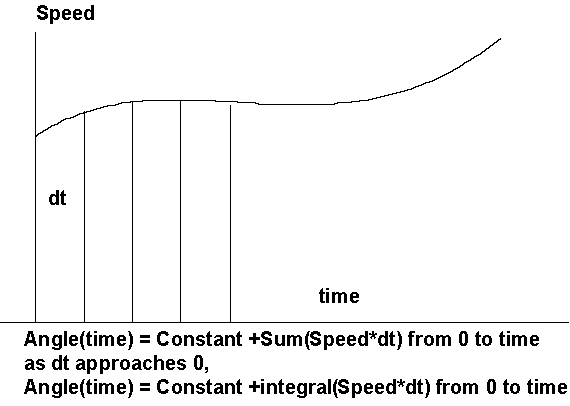
Figure 4: When Speed varies with time, it is necessary to integrate Speed to get the proper angle.

Fortunately, you don't need to do any work to get the sine/cosine functions because there is already a model in the ICAP/4 library that does all the work for you. It's called Voltage Controlled Oscillator (VCO), and it performs integration using a built-in Laplace function. The sine/cosine functions are made with behavioral elements. The model is described in detail in http://www.intusoft.com/nlhtm/nl67.htm#costas . The application for that Newsletter was a 900 MegHz communications receiver. Here, the same model is used but with frequencies below 1Hz!

The Encoder Model

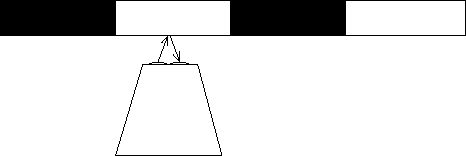
Marking the shaft with an alternating black and white pattern, shown in Figure 5 , allows an optical photo sensor to monitor shaft rotation.

Figure 5: A simple optically readable pattern

However, if the rotation direction is also needed, another sensor is usually added. Another pattern can also be added. The new pattern shown below (Figure 6) has the black and white stripes staggered. This arrangement is known as quadrature coding. If motion I is in the "forward" direction, then a 0-1 (black-white) transition in the "I" channel when the Q channel is false (black) is counted as a clockwise revolution. Conversely, a 1-0 transition counts as a counter-clockwise revolution. The logic reverses based on the quadrature channel so you can get 2 pulses for 1 pattern cycle.


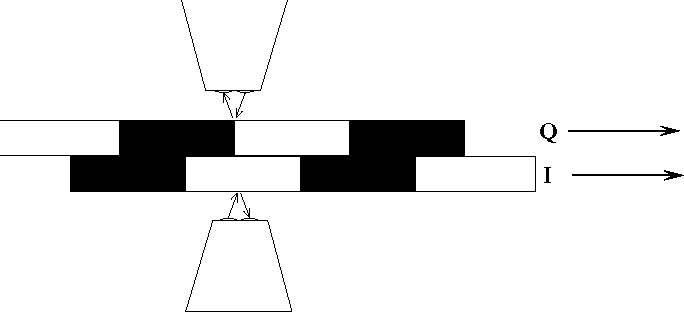
Figure 6: Adding a second pattern and sensor let's you count rotation in two directions.

Another way of building the quadrature signals is to stagger the sensors along a single pattern as shown in Figure_7. If half the shaft is painted white and the other half is painted black, separating the sensors by 90 degrees gives the desired result. The 90-degree separation places one of the signals in quadrature with the other.


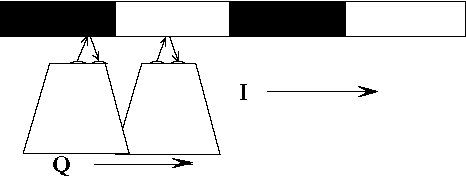
Figure 7: Staggering the sensors along a single pattern also works.
For shafts that are rotating, the x-y coordinate system was shown previously in Figure 3. The radial distance from the center of the shaft is given by r = x^2 + y^2. At an angle, A, y = r*sin(A) and x=r*cos(A). But with A, the shaft angle changes with respect to time. For a constant RPM, A increases with time just like the distance you drive at a constant speed. But the speed can increase or decrease, so you must integrate speed to obtain the correct angle. The VCO model is used to integrate the speed input and get the sine/cosine signals. The reflected optical signal has a cosine-tapered waveform because the illumination is a disc shaped light beam. As the pattern passes across the illuminating disc, the reflected light gradually changes from one state to the other with a cosine-like shape. The disc gets larger as the distance between the sensor and target pattern is increased and the spatial rise-time increases. If the light beam disc diameter is known along with the shaft diameter, then the spatial "rise-time" of the reflected signal can be calculated as follows:
Let Arise = angular rise "time"
DI = incident illumination diameter
DS=shaft diameter
Arise = DI / (pi*DS)

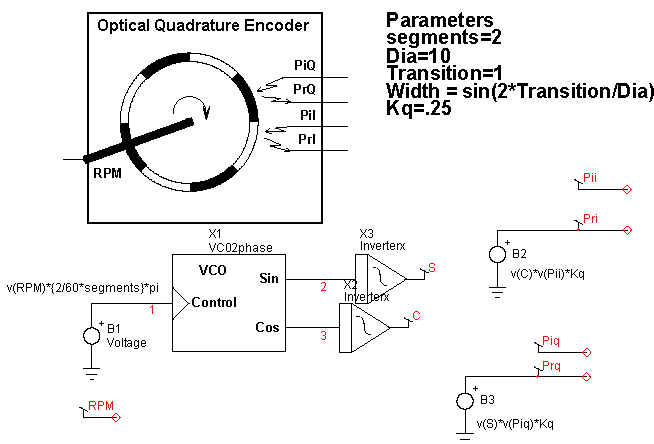
Now it is possible to have the pattern repeat in order to increase resolution. Yet, Arise is unaffected. But Arise will set an upper limit on the number of times the pattern can be repeated. Putting it all together in Figure 8 .

Figure 8: The complete encoder model and its symbol.

The ICAP/4 library models for VCO and invertex do exactly what is needed. VCO was developed for communications modulation and demodulation, while inverterx was made as a soft transition cosine shape limiter. The parameters passed into the model are:

Width: sets the transition behavior in inverterx.
Segments: sum of black and white bands to account for more pattern repetitions.
Kq: the reflection coefficient: If desired, you can sum noise, such as 120Hz signals from nearby incandescent and fluorescent lights. It's best if you shield the photo micro sensor from this source of noise. The one used here has an infrared filter to help eliminate visible light interference.
Dia: the encoder diameter (any units)
Transition: the distance between on-off detection (same units as Dia)

Designing the Decoder

So far, the project design has focused on getting an electro-optical interface that can act as a signal generator to test the project design. From the beginning, the I and Q signals are modeled with slow rise-times. Something must be done to sharpen these rise-times so they can be used as the clock for an up/down counter. Reviewing the available optical reflection sensors, there are some that have hysteresis limiters built-in. Hysteresis is a form of positive feedback that sharpens rise-times. The OMRON EE-SY413 is one such device. It was modeled using a previously developed opto-isolator with its optical path broken to output incident light and receive reflected light. Its current transfer ratio (CTR) was adjusted based on manufacturers data. Hysteresis was added using a SPICE3 behavioral switch. Initially it wasn't known if the rise-time of the device was as fast as required, but it was tested in the lab and found adequate for use as a clock for CMOS devices. It's now an ICAP/4 library item.

Next, the up/down counting logic needs to be designed. It's first necessary to know the current I and Q states, along with the previous states (called Ip and Qp). The reason behind this is to be able to detect a change in rotation direction soon after an up/down transition is made. These previous states are measured using delay multi-vibrator (DMV) constructed using CMOS inverters. The DMV uses positive feedback to make sharp transitions. These DMV transitions will form the active clock edge, which is the transition where the synchronous logic states are examined. The I, Ip, Q and Qp states can be drawn in a logic truth table, shown in Figure 9 . To make the truth table, take the I signal with its pattern of 0110. This pattern will repeat at the rotation frequency (RPM). Then, Ip is the previous pattern, 0011. Similarly you can enter the Q and Qp parts of the table. Next, reverse the rotation direction and make the second truth table.

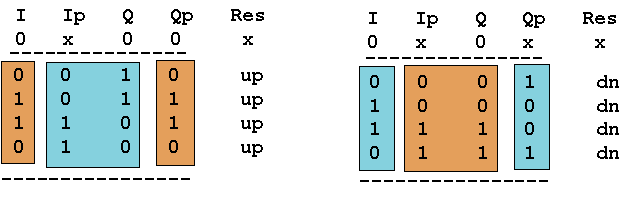
Figure 9 : Logic states for cw and ccw rotation.

The logic states have been shaded to show groupings that are useful. The cyan colored groups represent "exclusive or" patterns, while the brown shade shows "exclusive or not" groupings. By inspection we can write:

up = (I xor Qp)n &(Ip xor Q) and dn = (I xor Qp) & (Ip xor Q)n

Boolean Algebra Review

There are three basic Boolean operations. In engineering they are called AND, OR and NOT. Mathematicians call them intersection, union and negation, and use symbols that aren't on your keyboard to represent them. Sticking with engineering notation, we'll define the following operations:
AND
OR
NOT		 &
+
n

The exclusive or is encountered frequently enough to deserve its own operator; we'll use xor.

A truth table is a table of all interesting states and a corresponding result. A logic equation expresses the results as illustrated in the table below for some two-input results.

A
B
And2
A
B
Or2
A
B
Xor2
A
B
Xor2n
0
0
0
0
0
0
0
0
0
0
0
1
0
1
0
0
1
1
0
1
1
0
1
0
1
0
0
1
0
1
1
0
1
1
0
0
1
1
1
1
1
1
1
1
0
1
1
1
Table 1: Results for two input combinations
And2
Or2
Xor2
Xor2n		 =A & B
=A + B
=An & B + A & Bn
=(An&Bn + A&B)
 =(An + Bn)n
=(An & Bn)n
=(An&Bn + A&B)n
=(An & B + A & Bn)n

Notice that A&B+A&D = A&(B + D) so that OR follows algebraic rules for addition and AND follows algebraic rules for multiplication. The completed decoder circuit is shown below in Figure 10.


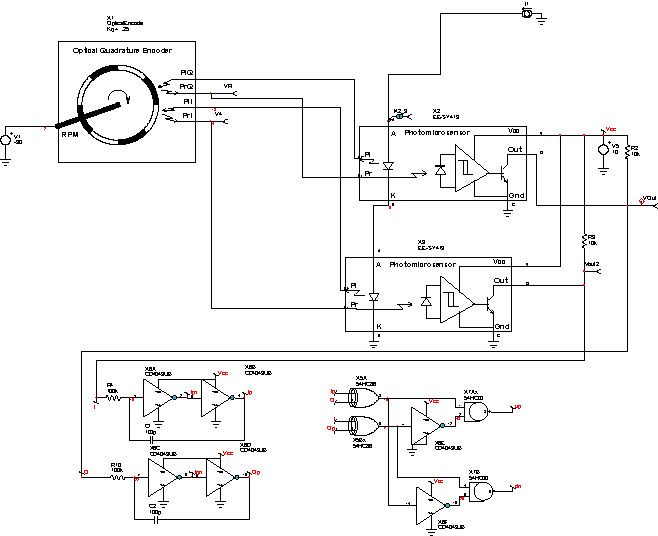
Figure 10: The complete decoder using the encoder model for testing.

The following waveforms below show the up/down counting pulses with a rotation reversal at 15 seconds.


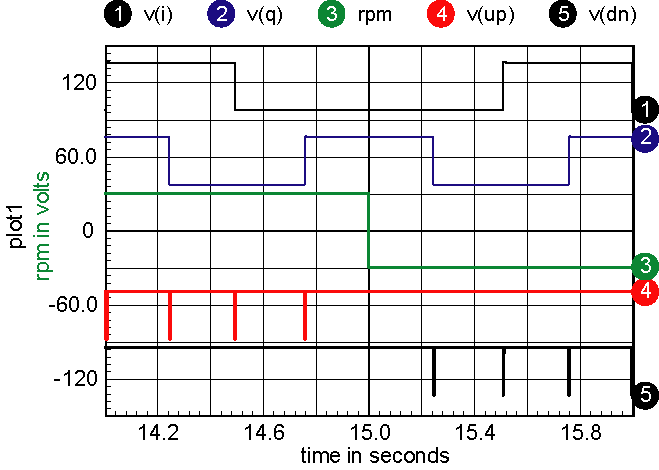
Figure 11: The up/down counting pulses with a rotation reversal at 15 seconds.

The up/down pulse widths are very short, so to see then using an oscilloscope, you must trigger on one of the I or Q signal edges and expand the trace to 100 microseconds.

Exclusive OR, where analog meets digital

Before moving on to the up/down counter and display circuitry, let's make a side trip to see how the technology that's been used here applies to several other applications. The exclusive OR is the basis for digital addition. It's fundamentally the sum of two bits. But from an analog perspective, if you let a logic "one" be defined as +1, and a logic "zero" as -1, then the exclusive OR is actually the product of the inputs. Using that property, taking two signals that are at the same frequency, but phase shifted, like the I and Q signals in the decoder, then the average value of the exclusive OR is proportional to the phase shift. That means that an analog phase detector can be formed using an exclusive OR and filtering the output with a low pass filter to get phase. When the signal to noise ratio is fairly high in a communications channel, you can limit the signal, turning it into a binary data stream. Then, an exclusive OR can be used to detect phase or frequency encoded signals. Of course, you don't really need +1 and -1 for logic levels, but using this thought process simplifies the math. Using CMOS for the logic is advantageous because the logic one and zero values are at the power supply rails, providing analog accuracy.

Looking further, suppose we want to use a laser to measure distance or speed. We can construct a Michelson Interferometer and place I and Q sensors ¼ wave apart on the fringe pattern. If the light wavelength is 1 micron (10^-6 meters), then you would obtain a 4 MegHz signal for a 1 meter/second velocity. The same thing can be done with radio waves or sound waves. The table below shows the sensitivity for 3 cases.

 
Wavelength
Frequency
Sensitivity
 
V/F
V/L
to 1 m/sec velocity
Optical
1u
3e14
4 megHz
Radio
.2
1.5g
20 Hz
Sound
.01
30 kHz
400 Hz

Table 2: Sensitivity

Note: For radio and optical applications c = 3*10^8 meters/second, for sound in the atmosphere, c is about 300m/sec (lots of pressure and temperature variation).

The optical detector is extremely sensitive and is being used by LIGO, the Laser Interferometer Gravitational Wave Observatory. Similarly, a fiber-optic coil can be used to detect vibration and/or rotation, making a sensitive microphone of a gyroscopic rotation sensor. The technique can be used to measure position from a GPS signal with accuracy on the order of 2cm (1/25th of a wavelength). Acoustic applications include ultrasound and sonar systems.

Some very simple equations blossom into an astonishing array of applications. Taking the math one step further leads to 3d-imaging systems and hologram construction; but that's for another time.

Counting the Pulses and Displaying the Results

To complete the project, the up/down pulses need to be counted and displayed. For an inexpensive stand-alone application it was decided to use CMOS logic. Alternatively, you could interface directly with your computer using a PIC (Programmable IC) connected to a USB port. A CD40192 Binary Coded Decimal (BCD) up/down counter accumulates 10 pulses per stage. It easily cascades to get the count as large as you want; our design used three stages to accumulate up to 1000 quarter turns. The BCD output is displayed by first decoding each digit to drive a 7 segment display. The seven segment display is a LITEON LSHD-7503. It's connected to the CD4511B Decoder using 470 ohm resistors that can be purchased in a 16 pin Dual in-line package (DIP). The parts can be interconnect using a Printed Wiring Board (PWB), soldering or wire wrapping. If you use a PWB, your probably want to use the Small Outline IC (SOIC) packages otherwise DIP packages are easier to work with.

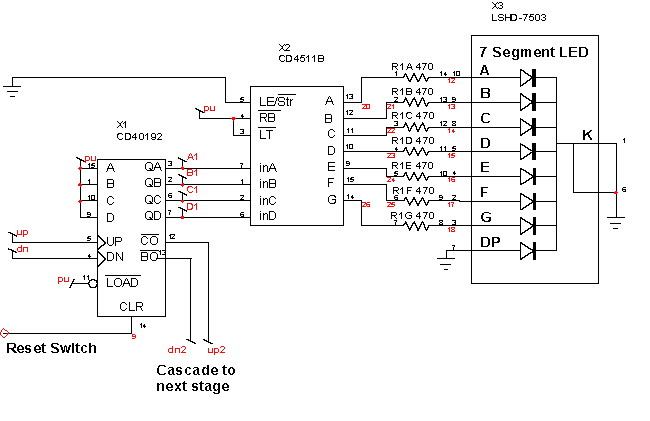
Figure 12: One of 3 stages of the counter and readout display